|
View: 5795|Reply: 9
|
Koleksi Soalan Terkumpul : Math
 [Copy link]
[Copy link]
|
|
|
SOALAN
1. Buktikan bahawa hasil darab dua nombor nyata negatif ialah suate nombor positif.
pendekatan aksiom memang boleh digunakan, dan soalan ini menjadi remeh. ttp pendekatan ini tidak sesuai pada peringkat awal, contohnya di tingkatan 1, di mana pelajar didedahkan kepada operasi algebra ini (terlalu abstrak utk tahap itu). Saya mencadangkan bukti ini:
Biar x, y dua nombor nyata dengan tanda yang sama. (sama-sama positif atau sebaliknya).
adalah benar bahawa:
-x + x = 0
darab kedua-dua belah dgn -y:
(-y)(-x) + (-y)(x) = 0
jadi (-y)(-x) = yx.
bukti ini hanya melibatkan pemahaman bahawa hasil darab satu nombor positif dengan negatif menghasilkan satu nombor negatif, dimana pelajar dapat faham dengan mudah (misalnya hutang $5 dengan 4 orang jadi jumlah hutang itu $20 (-20)).
_________________________________________________________
SOALAN
2. Buktikan ketaksamaan berikut.
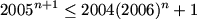
Penyelesaian ini adalah tepat. Terdapat 2 lagi cara untuk melakukan pembuktian : 1)Induksi ; 2) Ketaksamaan Holder.
mungkin saudara berminat mencuba.
________________________________________________________
SOALAN
3. Satu lagi... Buktikan ketaksamaan berikut
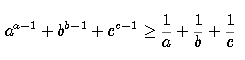
di mana a,b,c ialah nombor nyata positif
Saya minta maaf banyak banyak kerana terlupa menaip syarat "abc = 1". ttp ini telahpun kamu sedari (tajam...). pembuktian seterusnya hanya melibatkan penggunaan ketaksamaan e^x >= 1 + x.
SOALAN
4. Buktikan : n! >= n^n / n!
JAWAPAN Oleh perwiradua
Kita andaikan 0 < i <= n.
Terlebih dahulu buktikan [n-(i-1)] i >= n. Ianya akan jadi jelas kemudian.
Bukti:
------
[n-(i-1)] i - n = (n - i + 1) i - n
= ni - i^2 + i - n
= n(i-1) - i(i-1)
= (n-i)(i-1)
>= 0
sebab n-i >= 0 dan i-1 >= 0.
Dengan itu [n-(i-1)] i >= n.
Seterusnya,
(n!)^2 = [n(n-1)(n-2) ... 3.2.1][n(n-1)(n-2) ... 3.2.1],
tulis semula ungkapan sebelah kanan dengan memadankan sebutan-sebutan
seperti berikut:
[n(n-1)(n-2) ... 3.2.1][n(n-1)(n-2) ... 3.2.1]
= (n.1).[(n-1).2].[(n-2).3] ... [(n-(i-1)).i] ... [3(n-2)].[2(n-1)].(n.1)
>= n.n.n ... n ... n.n.n, (dari pembuktian sebelum ini),
= n^n, sebab terdapat n sebutan n.
Oleh itu (n!)^2 >= n^n atau n! >= n^n/n!.
SOALAN
5. Jika ab + bc + ac = 1, 0 < a, b, c < 1, buktikan: a / (1-a^2) + b/ (1 - b^2) + c / (1-c^2) ≥ (3√3) / 2
JAWAPAN oleh skanderbeg

p/s : Semua soalan dari skanderbeg dan jawapan soalan 1-3 dan 5 adalah dari skanderbeg manakala soalan 4 dari perwiradua
[ Last edited by adlismel at 27-12-2005 09:05 PM ] |
|
|
|
|
|
|
|
|
|
|
|
SOALAN 6 (Oleh WhiteShark)

Katakan sebiji roda bergolek dari kedudukan A ke A' yg membuat HANYA 1 pusingan lengkap.
Jadi jarak dari titik A ke titik A' adalah sama dgn lilitan LUAR roda tu kan.
Tapi bagaimana pulak dgn jarak dari titik a ke titik a'?
Kalau nampak secara kasar memang AA' = aa'.
Tapi lilitan LUAR roda tak sama dgn lilitan DALAM roda tu.
Boleh sape - sape jawab tak kemusykilan ni.
Soalan : macamana titik - titik pada lilitan DALAM roda tu bergerak di sepanjang garis lurus aa'?
* lilitan luar dan dalam masing - masing membuat satu pusingan penuh
JAWAPAN (Oleh : skanderbeg)
Dari segi sesaran memang
aa' = AA' *
jadi apa yang menyebabkan keadaan ini berlaku mestilah disebabkan oleh kadar putaran yang berbeza untuk titik A dan
titik a.
biar w(r) = putaran per unit masa untuk titik pada lilitan bulatan dalaman
t = jumlah masa untuk menyesarkan A ke A'
r = jejari bulatan dalaman
w(R) = putaran per unit masa untuk titik pada lilitan bulatan luaran
R = jejari bulatan luaran
perhatikan r ≦ R, dan 2兀r ialah sesaran per putaran (bulatan dalaman).
oleh sebab aa' = w(r) x t x 2兀r , AA' = w(R) x t x 2兀R
dengan hubungan *, diperoleh
rw(r) = Rw(R)
w(r) = R/r x w(R) ≧ w(R)
ketaksamaan ini menunjukkan bahawa kadar putaran untuk titik di lilitan bulatan dalaman adalah lebih cepat atau sama dengan titik di bulatan luaran. Kesamaan berlaku apabila r = R, iaitu apabila kita hanya mempertimbangkan titik pada lilitan bulatan luaran.
dengan kata lain, titik di lilitan bulatan dalaman dipaksa "bekerja keras" untuk mencapai sesaran yang sama bagi titik yang serenjang dengannya ttp berada di lilitan bulatan luaran |
|
|
|
|
|
|
|
|
|
|
|
SOALAN 7 (Oleh : ash_ikin)
Diberi R dan T masing2 ialah titik (0,5) dan (9,0) dan S ialah satu titik supaya RS selari dgn paksi-x dan OT = 3RS.
(a) nyatakan koordinat bagi titik S.
(b) cari panjang garis TR
(c) Hitungkan luas trapezium ORST, di mana 0 ialah asalan.
JAWAPAN (Oleh : candy )
HINT by candy
I assume RS is same direction as OT . Then since OT = 9 --> RS = 3 . So S (3,5)
b) use theorem phytagoras TR^2 = 9^2 + 5^2 = .....
c) Luas = 1/2 ( RS +OT) x RO = 1/2 (3+9) x 5 = ....
SOALAN 8 : (Oleh : ash_ikin)
Diberi p ialah satu punca bagi persamaan x^2 + (p-5)x -p^2 +7p - 3 = 0.
(a) Hitungkan nilai2 yg mungkin bagi p
JAWAPAN (Oleh : adlismel )
[color=sea green]Jawapannya seperti yang dinyatakan oleh candy
Persamaan x |
|
|
|
|
|
|
|
|
|
|
|
SOALAN 9 (Oleh : ash_ikin)
9. Diberi 3 titik P(6,4), Q(9,0) dan R(-2,0). Cari nisbah PT:TR, diberi T ialah titik persilangan PR dgn paksi-y.
JAWAPAN (Oleh : adlismel)
Cari dulu titik T (persilangan PR dgn paksi - y, maka x = 0)
Katakan P (6,4) ==> P (X1,Y1) dan R(-2,0) ==> R(X2,Y2)
Maka , ([Y - Y1] / [X - X1]) = ([Y2 - Y1] / [X2 - X1])
..:: ([Y - 4] / [X - 6]) = ([0 - 4] / [-2 - 6])
..:: ([Y - 4] / [X - 6]) = -4 / - 8
..:: ([Y - 4] / [X - 6]) = 1/2
..:: 2Y - 8 = X - 6
..:: 2Y = X - 6 + 8
..:: Y = ([X + 2]) / 2
Jika X = 0, maka Y = 1,
Maka titik T ialah (0,1)
Gunakan rumus [n(X2) + m(X2)] / (m + n)
[n(6) + m(-2)] / (m + n) = 0
(selesaikan dan hasilnya)
6n = 2n
m/n = 1/3
m:n = 1 : 3
Maka PT : TR = 3 : 1
SOALAN 10 (Oleh : ash_ikin)
10. Diberi lengkung y=kx^n melalui titik-titk (2,2) dan (5, 31), cari nilai k dan n.
JAWAPAN (Oleh : candy ( HINT))
ganti (2,2) dan (5,31) dan dpt dua psm iaitu
2 = k* 2^n -----(i) dan 31 = k*5^n ------(ii)
SOALAN 11 (Oleh : ash_ikin)
11. Diberi 3^2x - 3^x+2 - 3^x + 3^2 +0. Cari nilai-nilai x yg memuaskan persamaan tersebut.
JAWAPAN (Oleh : adlismel)
Rasanya macam nie (kalau tak tersilap)
..:: 3^2x - 3^(x+2) - 3^x + 3 |
|
|
|
|
|
|
|
|
|
|
|
SOALAN 12 (Oleh ash_ikin)
12. Garis lurus y= 4 - x bertemu dgn lengkung y= (x- p^2) pd titk di mana x=0. Diberi p ialah satu integer positif, cari nilai P dan koordinat-x bagi titik persilangan yg satu lagi.
Jawapan :-
y = 4 - x --------> (1)
y = x - p |
|
|
|
|
|
|
|
|
|
|
|
[quote]SOALAN 20 (Oleh :adlismel)
Sebuah kuboid mempunyai tapak berbentuk segiempat sama bersisi x cm. Tinggi kuboid itu adalah 1/2 kali panjang sisi tapaknya. Jika x bertambah dengan kadar 0.03 cm/s, carikan kadar perubahan isi padu kuboid itu apabila jumlah luas permukaannya ialah 1600 cm |
|
|
|
|
|
|
|
|
|
|
|
SOALAN 23 (Oleh : adlismel)
Ungkapkan 2 kos x - sin x dalam bentuk R kos (x + a) dengan R > 0 dan a ialah sudut tirus. Seterusnya selesaikan 2 kos x - sin x = 1 untuk 0 <= x <= 180
JAWAPAN (Oleh : BeanDiesel)
2 cos x - sin x = R cos (x + a) (so, kite nak solve for R and a)
2 cos x - sin x = R [ cos x * cos a - sin x * sin a] <-- pakai trig identity
2 cos x - sin x = R (cos x * cos a) - R (sin x * sin a) <-- ade dua equation kite leh dapat dari sini. first term of the left equation is a function of cos x and first term of the right equation is a function of cos x. 2nd term of the first equation is a function of sin x and the 2nd term of the right equation is a function of sin x. (R and a adalah konstant).
2 cos x = R (cos x * cos a) .... (1)
-sin x = -R (sin x * sin a) .... (2)
from equation (1)
cancel cos x from each side of the equation
2= R cos a
R = 2/cos a |
|
|
|
|
|
|
|
|
|
|
|
SOALAN 25 (Oleh : adlismel)
2^x - 1/16^x = 0
JAWAPAN (Oleh : Satria-Naga)
1. 2^x - 1/16^x = 0 [/quote]

Cara 1
2^x - 1/16^x = 0
2^x - 2^-4x = 0
2^x = 2^-4x
Bandingkn indeks,
x=-4x
x=0
Cara 2
2^x - 1/16^x = 0
2^x - 1/2^4x = 0
2^5x - 1 = 0
2^5x = 1
2^5x = 2^0
Bandingkn indeks,
5x = 0
x = 0
SOALAN 25 (Oleh :adlismel)
Selesaikan Persamaan 2 * 5^x = 3^(x - 1)
JAWAPAN (Oleh : BeanDiesel & Satria - Naga)
2* 5^x = 3^(x - 1)
2* 5^x = 3^x / 3^1
= 3^x/ 3
2* 3 = 3^x / 5^x
6 = (3/5)^x
log(6)=log ( (3/5)^x )
=x log (3/5)
x= log (6) / log (3/5)
x is about -3.50758.....
2nd answer by SN
2* 5^x = 3^(x - 1)
log 2* 5^x = log 3^(x - 1)
log 2 + log 5^x = (x - 1) log 3
log 2 + x log 5 = x log 3 - log 3
x log 3 - x log 5 = log 2 + log 3
x log (3/5) = log 6
x = log 6 / log (3/5)
x = -3.5076
SOALAN 26 by ash_ikin
1) Diberi g(x)=3x+2 dan gf(x)=11-3x. Hitungkan nilai-nilai w jika fg(w^2+2)=7x-11.
JAWAPAN by BeanDiesel
(a)
g(x) = 3x + 2
g(s) = 3s + 2 <---kita tak ubah pon function ni, just tuka variable tanak kasi keliru.
g[f(x)] = 11 - 3x <--dalam function ni f(x) ialah variable utk fungsi g, ataupon f(x) = s
g[f(x)] = 11 - 3x = 3s + 2
s = 3 - x = f(x)
so, f(x) = 3 - x
g(x) = 3x + 2
kita nak f[g(x)], maknana g(x) ni jadi variable dalam f(x)
f[g(x)] = 3 - (g(x)) = 3 - (3x+2)
f[g(x)] = 1 - 3x
(b) Hitungkan nilai-nilai w jika fg(w^2 + 2)= 7w-11
skrg, w^2 + 2 jadi variable dalam f[g(x)]
f[g(w^2 + 2)] = 1 - 3(w^2 + 2) = 7w-11
1 - 3w^2 - 6 = 7w - 11
3w^2 + 7w -6 = 0
cari nilai nilai w guna w=[ -b +/- sqrt (b^2 - 4ac) ]/ 2a
a = 3, b=7, c=-6
w = [-7 +/- sqrt(49 + 72) ] / 6
w =[ -7 +/- 11 ]/6
w = 2/3 & -3
SOALAN 27 by ash_ikin
2) Diberi p dan p+3 ialah punca-punca persamaan kuadratik 2x^2 +14x +k =0. Cari nilai pdan k.
JAWAPAN by BeanDiesel
2x^2 +14x +k =0
= x^2 + 7x + (k/2) ....(1)
ok, now p dan p+3 adalah punca persamaan quardratic. so kite boleh tulis p dan p+3 camni,
(x - p) (x - [p+3]) = 0 = x^2 + 7x + (k/2) <-- perhatikan dalam (x - p) (x - [p+3]) , gandaan x ialah 1, dan dalam persamaan kuardratik tu, gandaan x^2 ialah satu. so senang la nak compare kedua dua equation ni.
so, kembangkan (x - p) (x - [p+3])
= x^2 - x(p+3) - px + p(p+3)
= x^2 - x(p+3+p) + (p^2 + 3p)
=x^2 - x(2p+3) + (p^2 + 3p).....(2)
bandingkan (1) & (2)
x^2 - x(2p+3) + (p^2 + 3p) = x^2 + 7x + (k/2)
so kite boleh dapat dua equation dari sini
1) -x(2p+3) = 7x <--cancel x from both sides
-(2p+3) = 7
p = -5
2) (p^2 + 3p) = k/2
k = 2(p^2 + 3p) <--masukkan nilai p yang kite dapat tadi
k = 20
SOALAN 28 by ash_ikin
3) Satu drp punca persamaan 2x^2+12x=6k-1 ialah 2 kali yang satu lagi dgn keadaan k adalah pemalar. Cari punca-punca tersebut dan nilai k.
JAWAPAN by adlismel
SOLUTION
2x^2+12x=6k-1 ==> 2x |
|
|
|
|
|
|
|
|
|
|
|
[quote]SOALAN 31 by adlismel
Cari nilai t jika y = 10 ialah tangen kepada lengkung y = x |
|
|
|
|
|
|
|
|
|
| |
Category: Belia & Informasi
|