|
View: 7691|Reply: 26
|
Bagaimana Pembuktian Rumus Matematik disahkan
[Copy link]
|
|
|
Aku baru ajar bab Pembezaan untuk Petua hasil darab dan hasil Bahagi.. bila aku tengok cara pembuktian rumus tu aku kurang setuju sikit yajng ada dalam buku teks tingkatan 4.
macam mana rumus matematik ni mendapat kesahan daripada semua pihak? |
|
|
|
|
|
|
|
|
|
|
|
|
bagi contoh skit... tak da buku form 4 la |
|
|
|
|
|
|
|
|
|
|
|
oh Adli
|
yg FermaT LAst THeorem tu betul ker Andrew Wiles dah buktikan? |
|
|
|
|
|
|
|
|
|
|
|
|
aku pun tak tau,,,, heeeee.. tu yang aku nak tanya kat korang semua nie |
|
|
|
|
|
|
|
|
|
|
|
contoh rumus
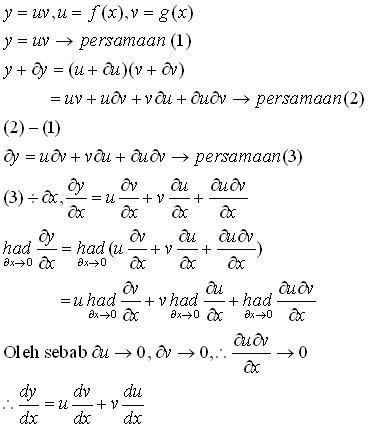 |
|
|
|
|
|
|
|
|
|
|
|
|
macam mana dia terus terbuktikan yang akhir sekali tu |
|
|
|
|
|
|
|
|
|
|
|
|
oleh sebab.... terus terbukti rumus tu |
|
|
|
|
|
|
|
|
|
|
|
"bukti" ini sebenarnya bukan bukti yang rapi. Untuk itu anda memerlukan kalkulus lanjutan.
"Bukti" ini diberi kerana bukti asal dianggap terlalu sukar difahami utk pelajar tingkatan 4 oleh "pakar" di kementerian.
bukti ini hanya melibatkan sedikit manipulasi algebra, dan konsep "tokokan kecil" diperkenalkan.
Ternyata sebutan terakhir menghampiri sifar kerana (delta u / delta x ) akan menumpu kepada du/dx (malar), manakala delta v (tokokon kecil sebarangan) menghampiri sifar.
kelemahan terbesar bukti ini ialah ia tidak memberikan gambaran yg jelas tentang apakah maksud pembezaan yang sebenar.
Bukti yg rapi adalah begini:
takrif terbitan suatu fungsi licin f(x) ialah:
df(x) / dx = lim_{h -> 0} [ { f(x+h) - f(x) } / h ]
takrif ini adalah semulajadi krn ia menunjukkan bahawa pembezaan pada mana mana titik untuk satu fungsi licin melibatkan proses di mana satu garis sekant (secant line) digerakkan sedemikian sehingga garis itu membentuk garis tangent kepada satu titik pada fungsi licin itu. Kecerunan, segitiga dan konsep had terlibat dalam hal ini.
jadi, d (f(x)g(x)) / dx = lim_{h -> 0} [ { f(x+h)g(x+h) - f(x)g(x) } / h ]
= lim_{h -> 0} [ { f(x+h)( g(x) + g(x+h) - g(x) ) - f(x)g(x)} / h ]
= lim_{h->0} [ {f(x+h)g(x) + f(x+h)(g(x+h) - g(x)) - f(x)g(x)} / h ]
= lim_{h->0} {g(x)(f(x+h) - f(x))} / h + { f(x+h)(g(x+h) - g(x))} / h
= g(x) df(x)/dx + f(x) dg(x)/dx
di mana langkah terakhir diperoleh berdasarkan takrif terbitan dan juga fakta bahawa f(x+h) -> f(x) apabila h ->0.
P/S: Bukti Andrew Wiles telah diperiksa oleh antara pakar matematik terkemuka di dunia dan tidak ada sangkalan munasabah yg wujud dlm pembuktiannya. Jadi sudah diterima bahawa masalah fermat terakhir itu diselesaikan. Dianggarkan tidak lebih drp 20 org (atau kurang) di dunia ini yg mampu memahami bukti itu.
Sebelum itu byk org yg mendakwa berjaya menyelesaikan masalah fermat ttp "bukti" mereka mempunyai kesilapan atau kelemahan yg tidak dapat diperbaik. Kalau tak silap saya, dulu (lebih 10 thn dulu!) saya pernah membaca berita tentang seorang ahli matematik melayu yg mendakwa beliau menyelesaikan masalah itu...lupa namanya. |
|
|
|
|
|
|
|
|
|
|
|
Originally posted by mbhcsf at 8-9-2005 02:30 PM
yg FermaT LAst THeorem tu betul ker Andrew Wiles dah buktikan?
memang dah dibuktikan oleh wiles ini,saya pada tahun 1993 kat Persidangan Teori Nombor di Universiti Cambridge,England. |
|
|
|
|
|
|
|
|
|
|
|
emmm... aku rasa kita tak perlu pergi jauh...
kalau kita faham apa tu ∂, d dan D.. aku rasa sudah memadai untuk kita faham pembuktian tu (sbb. yg last tu mmg telah dibuktikan). |
|
|
|
|
|
|
|
|
|
|
|
Originally posted by skanderbeg at 10-9-2005 08:06 PM
"bukti" ini sebenarnya bukan bukti yang rapi. Untuk itu anda memerlukan kalkulus lanjutan.
"Bukti" ini diberi kerana bukti asal dianggap terlalu sukar difahami utk pelajar t ...
ahli matematik melayu yang mendakwa menyelesaikan/membuktikan format tu dalam satu mukasurat ke???? |
|
|
|
|
|
|
|
|
|
|
|
Originally posted by skanderbeg at 10-9-2005 08:06 PM
"bukti" ini sebenarnya bukan bukti yang rapi. Untuk itu anda memerlukan kalkulus lanjutan.
"Bukti" ini diberi kerana bukti asal dianggap terlalu sukar difahami utk pelajar t ...
Ok... mmeang susah sikit nak faham... |
|
|
|
|
|
|
|
|
|
|
|
kehkeh
x masuk form 4 lagi |
|
|
|
|
|
|
|
|
|
|
|
Originally posted by rudz at 11-9-2005 11:13 AM
emmm... aku rasa kita tak perlu pergi jauh...
kalau kita faham apa tu ∂, d dan D.. aku rasa sudah memadai untuk kita faham pembuktian tu (sbb. yg last tu mmg telah dibuktikan).
Masalah, apabila ditulis
lim_{∂x ->0} ∂y/∂x = dy/dx maka apakah sebenarnya yang difahami? sebaliknya, ia seolah-olah silap mata matematik, yg hanya akan menambahkan keresahan pelajar.
pada hemah saya, bukti asal bukannya terlalu sukar untuk difahami, malah mempunyai kelebihan krn menggunakan hujah geometri. |
|
|
|
|
|
|
|
|
|
|
|
Originally posted by skanderbeg at 12-9-2005 09:24 AM
lim_{∂x ->0} ∂y/∂x = dy/dx maka apakah sebenarnya yang difahami? sebaliknya, ia seolah-olah silap mata matematik, yg hanya akan menambahkan k ...
emm.. nak cakap bahasa matematik nie susah skit (sorryla dah lama tinggal skolah)
anyway.. boleh cakap macam nie kot,
dy/dx nie adalah kadar perubahan y terhadap perubahan x ( ie. (y2 - y1)/(x2 - x1) dimana f(x2,y2) = (x2,y2) dan f(x1,y1)=(x1,y1) ). So, apabila ianya "kadar" bermaksud ianya adalah satu constant??? contohnya 10 m/s, 2xy J/kg dsbnya. Lanjutan dari itu, bagi membuat pembuktian satu "kadar" tu... ianya kena mempertimbangkan "value" dari yang sekecil mungkin hingga sebesar gila (∞). Bagi "value" yang sebesar gila ( ∞), operasi matematik tu menjadi "meaningless", dari itu.. cukup sekadar sekecil mungkin.
emmm.. boleh faham ke apa yg aku tulis nie... (aku pun dah confuse nie...) |
|
|
|
|
|
|
|
|
|
|
|
Originally posted by rudz at 12-9-2005 10:17 PM
emm.. nak cakap bahasa matematik nie susah skit (sorryla dah lama tinggal skolah)
anyway.. boleh cakap macam nie kot,
dy/dx nie adalah kadar perubahan y terhadap perubahan x ( ie. (y2 - y1) ...
Ok.. memang betul.... pembezaan adlah satu nilai penghampiran sama ada yang terkecil sehingga terbesar.... |
|
|
|
|
|
|
|
|
|
|
|
Originally posted by rudz at 12-9-2005 10:17 PM
dy/dx nie adalah kadar perubahan y terhadap perubahan x ( ie. (y2 - y1)/(x2 - x1) dimana f(x2,y2) = (x2,y2) dan f(x1,y1)=(x1,y1) ). So, apabila ianya "kadar" bermaksud ianya adalah satu constant??? contohnya 10 m/s, 2xy J/kg dsbnya. Lanjutan dari itu, bagi membuat pembuktian satu "kadar" tu... ianya kena mempertimbangkan "value" dari yang sekecil mungkin hingga sebesar gila (∞. Bagi "value" yang sebesar gila ( ∞, operasi matematik tu menjadi "meaningless", dari itu.. cukup sekadar sekecil mungkin.
Konsep terbitan melibatkan kuantiti yang amat kecil (infinitesimal), dan bukan sebaliknya.
mengatakan bahawa " dy/dx nie adalah kadar perubahan y terhadap perubahan x ..." ialah satu bentuk deskripsi, bukan penjelasan. Ini sama seperti bertanya mengapa daun itu hijau, lalu dijawab "krn ia mengandungi klorofil".
ternyata ini hanya satu deskripsi. Mengapa klorifil itu hijau??
Penjelasannya datang dari fizik : molekul klorofil itu hijau kerana ia menyerap gelombang yang sepadan dgn warna lain, tetapi memantulkan gelombang yang sepadan dgn warna hijau. Jadi mata kita mengesan gelombang ini dan mentakrifkannya sebagai hijau.
Jadi penjelasan harus berbalik kpd takrif matematik terbitan. |
|
|
|
|
|
|
|
|
|
|
|
Originally posted by skanderbeg at 13-9-2005 11:48 AM
Konsep terbitan melibatkan kuantiti yang amat kecil (infinitesimal), dan bukan sebaliknya.
Sefaham saya konsep ini melibatkan daripada sekecil mungkin sehingga sebesar mungkin (sorryla.. saya x mempunyai hujah yg 'concrete' memandangkan dah lama tinggal & tiada bahan rujukan.)
Bagi saya
lim_{∂x ->0} ∂y/∂x = dy/dx; pernyataan ini nampak ganjil/gonjeng (saya x ingat pun ada teorem sebegini; even saya tak bleh recall apa nama teorem ini, sapa jumpa dan bila).
Serasa saya pernyataan yg sepatutnya adalah;
Diberi; lim_{∂x ->0} ∂y/∂x = lim_{∂x ->0} (u ∂v/∂x + v ∂u/∂x + ∂u∂v/∂x)
Biar; lim_{∂x ->0} ∂y/∂x = dy/dx , lim_{∂x ->0} ∂u/∂x = du/dx, lim_{∂x ->0} ∂v/∂x = dv/dx, lim_{∂x ->0} ∂u∂v/∂x = 0 (oleh kerana ∂u -> 0, ∂v -> 0 maka ∂u∂v - > 0 )
Jika ; lim_{∂x ->0} ∂y/∂x = lim_{∂x ->0} (u ∂v/∂x + v ∂u/∂x + ∂u∂v/∂x) (1)
Maka ; dy/dx = udv/dx + vdu/dx (2)
Serasa saya isu yang sebenarnya (dalam bahasa biasa la kan) apa yg dibuktikan oleh wiles adalah sifat bagi pernyataan (1) adalah sama seperti sifat bagi pernyataan (2). Dengan kata lain, pernyataan (1) boleh diwakilkan dengan pernyataan (2) atas nama sifat dan kelakuan pernyataan tersebut.
Hujah saya yg kedua.
teorem lim_{∂x ->0} ∂y/∂x = dy/dx ini adalah mustahil/tidak wujud. Kalau ada dlm buku teks tu diaorang akan tulis terus.
p/s. boleh faham ke mantik saya |
|
|
|
|
|
|
|
|
|
| |
Category: Belia & Informasi
|